1最有影响力的期权定价公式：布莱克-斯科尔斯公式

 

 C: 期权合理价格；

S: 标的证券当前价格；

E: 期权的行权价格；

T：期权行权日日期；

t：使用公式当时的日期；

r：连续复利计的无风险利率 ；

标的证券连续复利回报率的年度波动率。

 

布莱克斯科尔斯公式提供了一种欧式期权的理论价值计算方法，它源于布莱克-斯科尔斯模型。1997年10月10日，模型创立者罗伯特·莫顿（Robert Merton）和迈伦·斯科尔斯（Myron Scholes）获诺贝尔经济学奖。

 

2 期权理论价格影响因素

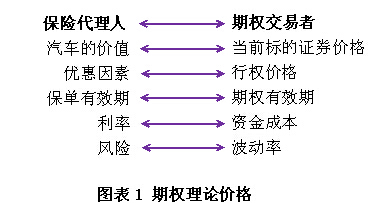
该模型比较复杂，我们可以简单地类比和汽车保险来理解它。两者都主要取决于：

• 资产的价值（汽车或者现货）
• 风险（您的驾驶记录或者是现货的平均价格变化）

对比驾驶者甲和驾驶者乙：

• 驾驶者甲是一个17岁的男高中生，自从拿到驾照之后，已经吃了两张超速罚单。他的父母给他买了一辆法拉利，保险杠上贴着：“我开不了太慢”。
• 驾驶者乙是一个35岁的家庭主妇，开一辆本田雅阁，在过去十年都没有交通违规。

很显然，谁的风险更大、保费更高？保险代理人甚至会拒绝给驾驶者A提供保险。

 

    让我们将汽车保险与某商品的期权价格做如下对比，按上述公式计算看涨、看跌期权理论价格，并分析影响因素，见图表1：

 

期权定价计算器
商品现货价格 = 2100元	看涨期权 22.87元
行权价格 = 2100元
时间 = 30天
无风险利率 = 4%	看跌期权 15.90元
分红率 = 0
波动率 = 8%

 

2.1 标的证券价格的影响

商品期货的期货结算价与现货有很高的相关度。如果现货上涨，那么期货、期权多头都随之上涨，反之相反，见图表2。

标的商品现货价格是影响期权价值最重要的因素，而且波动及其剧烈，因为其衍生品的属性。期权这种衍生品主要是反映未来买卖现货的权利。

 

图表2 标的证券对期权价格的影响

 

2

 

2.2 行权价的影响

 

行权价是允许投资者行权的价格，即买或卖标的现货的价格。它就像汽车保险中可抵扣的项目。可抵扣额度的变化将剧烈影响保险价格。

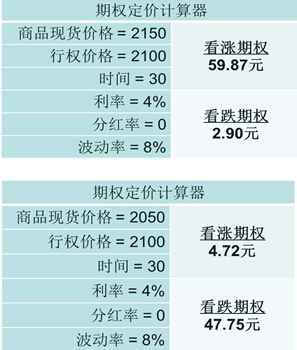
看涨期权是买入的权利，因此行权价比目前现货还低的看涨期权明显具有价值。如果现货目前在2100元，那么行权价2050元的看涨期权比行权价2150元的看涨期权价值大很多，见图表3。

对于看跌期权，情况相反。行权价比标的现货高的看跌期权价值更大，因为他们是卖出的权利。注意：看涨期权和看跌期权随着行权价不同而波动。

 

图表3 行权价对期权价格的影响

期权定价计算器
商品现货价格 = 2100	看涨期权 5.06元
行权价格 = 2150
时间 = 30
利率 = 4%	看跌期权 47.92元
分红率 = 0
波动率 = 8%

 

期权定价计算器
商品现货价格 = 2100	看涨期权 59.50元
行权价格 = 2050
时间 = 30
利率 = 4%	看跌期权 2.69元
分红率 = 0
波动率 = 8%

 

2.3 剩余时间的影响

到期时间：在多长时间后期权将结束的时间长度。到期时间90天的期权一定比30天的更有价值么？这是一个策略问题，市场上还有90天到期的期权比还剩30天的价值一定更大，见图表4。

注意：期权价值随时间非线性地变化。也就是说90天比30天长三倍，但价值并不是高3倍。

 

图表4 剩余时间对期权价格的影响

期权定价计算器
商品现货价格 = 2100	看涨期权 22.87元
行权价格 = 2100
时间 = 30
利率 = 4%	看跌期权 15.90元
分红率 = 0
波动率 = 8%

 

期权定价计算器
商品现货价格 = 2100	看涨期权 44.54元
行权价格 = 2100
时间 = 90
利率 = 4%	看跌期权 23.75元
分红率 = 0
波动率 = 8%

 

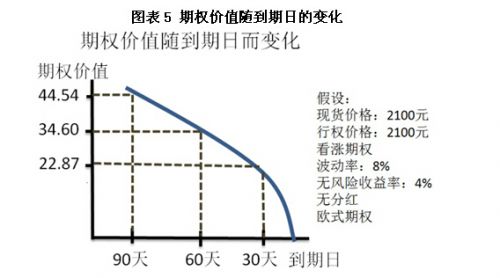
时间会影响期权的价格。事实上，如果商品现货价格不变，期权价值会随着到期日的临近而降低。这个概念就叫做时间价值或时间损耗。

作为期权的多头或空头，您在期权交易时必须考虑期权价值的时间损耗，以便选择最符合您的交易策略的期权。附图中说明了此期权从到期90天到到期日的价格变化。注：在到期之前的最后30天，时间价值非线性变化，并归零，见图表5。

 

图表5 期权价值随到期日的变化

 

3

 

2.4 无风险利率的影响

利率很重要，因为货币总可获得无风险收益率。期权定价时，由于期权的创造者往往要融资买入或卖出某种资产，而融来的资金需要支付借款利息，因此融资成本必须考虑，而期权价格中包括融入款的利息成本。

随利率上升，看涨期权价值上升，看跌期权价值下降，这是因为卖出看涨期权的人由于需要提前买入标的现货，需要借款，产生了利息，这部分利息支出转移到了看涨期权上。这点从期权定价公式中也可以看出，见图表6.

 

图表6 无风险利率对期权价格的影响

期权定价计算器
商品现货价格 = 2100	看涨期权 22.87元
行权价格 = 2100
时间 = 30
利率 = 4%	看跌期权 15.90元
分红率 = 0
波动率 = 8%

 

期权定价计算器
商品现货价格 = 2100	看涨期权 26.90元
行权价格 = 2100
时间 = 30
利率 = 8%	看跌期权 13.00元
分红率 = 0
波动率 = 8%

 

 

2.5 波动率的影响

波动率影响着标的资产在一天、一周或一年中波动情况的。同时，它也是定价公式、交易策略、整个市场中唯一未知的变量。这是您及整个市场需要预测的一个变量。举例来说，对于驾驶员A，接下来30天内，他遇到交通事故的可能性是10%？30%？或50%？这无法获知，但您必须预测。

对于某种商品期货现货8%的波动率，含义：当前点位是2100元时，在大部分情况下，现货将在1932点到2268点的范围内交易。这可能正确，可能错误。随着波动率的增加，看涨期权和看跌期权的价值都将增加，如图表7。

 

图表7 波动率对期权价格的影响

期权定价计算器
商品现货价格 = 2100	看涨期权 22.87元
行权价格 = 2100
时间 = 30
利率 = 4%	看跌期权 15.90元
分红率 = 0
波动率 = 8%

 

期权定价计算器
商品现货价格 = 2100	看涨期权 41.95元
行权价格 = 2100
时间 = 30
利率 = 4%	看跌期权 37.97元
分红率 = 0
波动率 = 16%

 

如果您交易过股票，您可能已经理解了波动率。在现货的世界里，这其实就是风险。商品现货价格波动越大，风险也就越大，而以此为标的的期权价值也就越大。

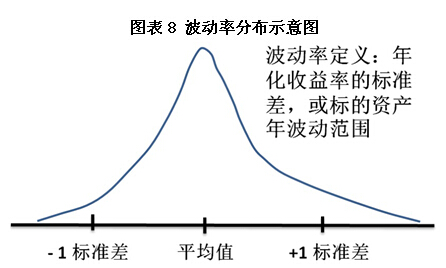
对于现货来说，价格波动是按波动的方向和波动的幅度来衡量。对于期权波动率来说，我们只关注价格波动的幅度，而不是方向。波动率反映平均和预期价格变动幅度的一个百分数，如图表8。

 

图表8 波动率分布示意图

 

4

 

2.6  实值期权、平值期权和虚值期权（Moneyness）

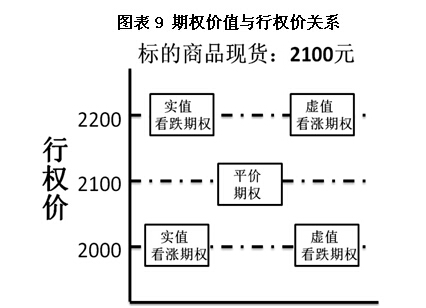
实值期权：对看涨期权：行权价格低于标的商品现货价格；对看跌期权：行权价格高于标的商品现货价格。

虚值期权：对看涨期权：行权价格高于标的商品现货价格；对看跌期权：行权价格低于标的商品现货价格。

平值期权：行权价格等于商品现货市场价格。如图表9.

 

图表9 期权价值与行权价关系

 

5

只有实值期权有内在价值，对于一个行权价格为2100元、而市价为2200元的看涨期权，其至少对应100元价值，持有者可立刻执行期权的权利，以2100元的价格买入现货，并以2200元卖出，赚100元。

但期权的价值不止于此，这是因为无论是实值、平值和虚值期权，都有时间价值。时间价值是由于标的证券可能的价格波动产生的额外价值，如图表10.

 

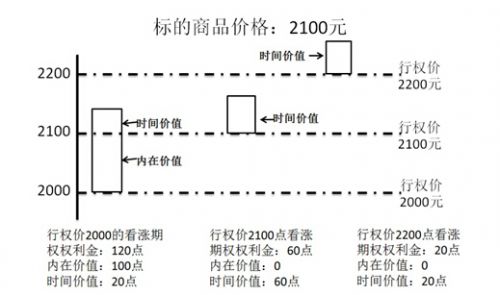
图表10 行权价、剩余时间对期权价格的影响

 

6

如果行权价格2100元的看涨期权，其现货为2200元，权利金为120元，那么其中有100元对应实值部分，20元为时间价值。这额外的20元，归咎于现货潜在的波动率（也就是说它可能还上涨）。

对于标的现货2100元，行权价格为2100元，看涨期权权利金60元，这60元完全对应波动率价值和时间价值；同理，对于标的现货2100元，行权价2200元，看涨期权20元，那么这20元也仅对应波动率价值和时间价值。

期权的价值不可能为负，内在价值和时间价值都不可能为负。

 

2.7 波动率的描述：用5个希腊字母估算期权理论价格

  Delta值 - 当标的证券发生1单位变化时，期权理论价值的变化量

Γ Gamma值 - 当标的证券发生1单位变化时，期权Delta的变化量。

Θ Theta值 - 期权价格的变动相对于时间变化的比率.

Κ Vega值 - 当波动率变化1单位（1%）时，期权理论价值的变化量。

Ρ Rho值 - 当利率变化1%时，期权理论价值的变化量

2.7.1 Delta值

 

期权价格变化速率用Delta表示。当标的证券上涨时，看涨期权的Delta值将增加，看跌期权的Delta值将减少。若Delta值为0.50，意味着标的证券价格上涨或下跌1元，期权的价格将变动0.5元

例：假设Delta=0.50， 当标的证券升高或降低1元时，其期权升高或降低0.50元，见下表：

	看涨期权	看跌期权
理论价格	3.50	3.25
Delta:	0.561	-0.439
Gamma:	0.045	0.045
Theta:	-0.140	-0.121
Vega:	0.095	0.095
Rho:	0.055	-0.070

期权快要到期时，实值期权的和虚值期权的Delta值将不同。实值期权趋向于100%，虚值期权趋向于0%，如图表11。

 

图表11 实值、虚值期权Delta不同变化

 

 

2.7.2 Gamma值

Gamma表示当标的证券价格发生1单位变化时，期权Delta的变化量。与Delta类似，Gamma也是通过百分比的形式来表示。下例是一个标的证券价格为50元，执行价50元的期权的希腊字母示例。

说明:  股价每涨价1元，看涨期权的Delta值增加0.045 ，看跌期权的Delta值也增加0.045，见下表。

	看涨期权	看跌期权
理论价格	3.50	3.25
Delta值:	0.561	-0.439
Gamma值:	0.045	0.045
Theta值:	-0.140	-0.121
Vega值:	0.095	0.095
Rho值:	0.055	-0.070

 

2.7.3 Theta值

Theta是用来测量时间变化对期权理论价值的影响；权利金衰减的速率；表示每经过一天，期权价值会损失多少；Theta随着到期时间的临近，呈现货型上涨；期权卖方有正的Theta，而期权买方的Theta是负的。

Theta = 期权价格变化/距离到期时间的变化；

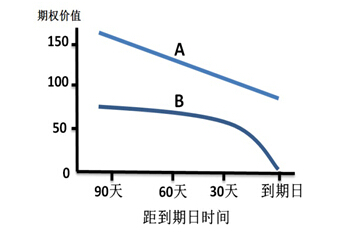
由于只有时间价值是损耗的，具有更大内在价值的期权，其价值随时间靠近到期日的变化曲线更加平缓。例如：假设到期日某种商品期货现货2100元，对行权价格2000元的看涨期权A和行权价格2100元的看涨期权B，期权A的价值随时间减少而导致的价值下降将更平缓，见图表12。

 

图表12 不同商品期权随到期日的临近理论价值变化

 

7

 

2.7.4 Vega值

Vega表示波动率的变化，单位：元，表示由于波动率变化而导致的期权价格变化量。例: 如果一个期权的标的资产从 60元降到59元,我们估计看涨期权和看跌期权的价格都将下跌0.095 元，如下表。

	看涨期权	看跌期权
理论价格:	3.50	3.25
Delta值:	0.561	-0.439
Gamma值:	0.045	0.045
Theta值:	-0.140	-0.121
Vega值:	0.095	0.095
Rho值:	0.055	-0.070

 

2.7.5 Rho值

Rho描述的是当利率变化1%时，期权理论价格的变化量。例: 如果利率从5.11%降到4.11%，看涨期权和看跌期权的理论价格达到3.45元和3.32元。

	看涨期权	看跌期权
理论价格:	3.50	3.25
Delta值:	0.561	-0.439
Gamma值:	0.045	0.045
Theta值:	-0.140	-0.121
Vega值:	0.095	0.095
Rho值:	0.055	-0.070